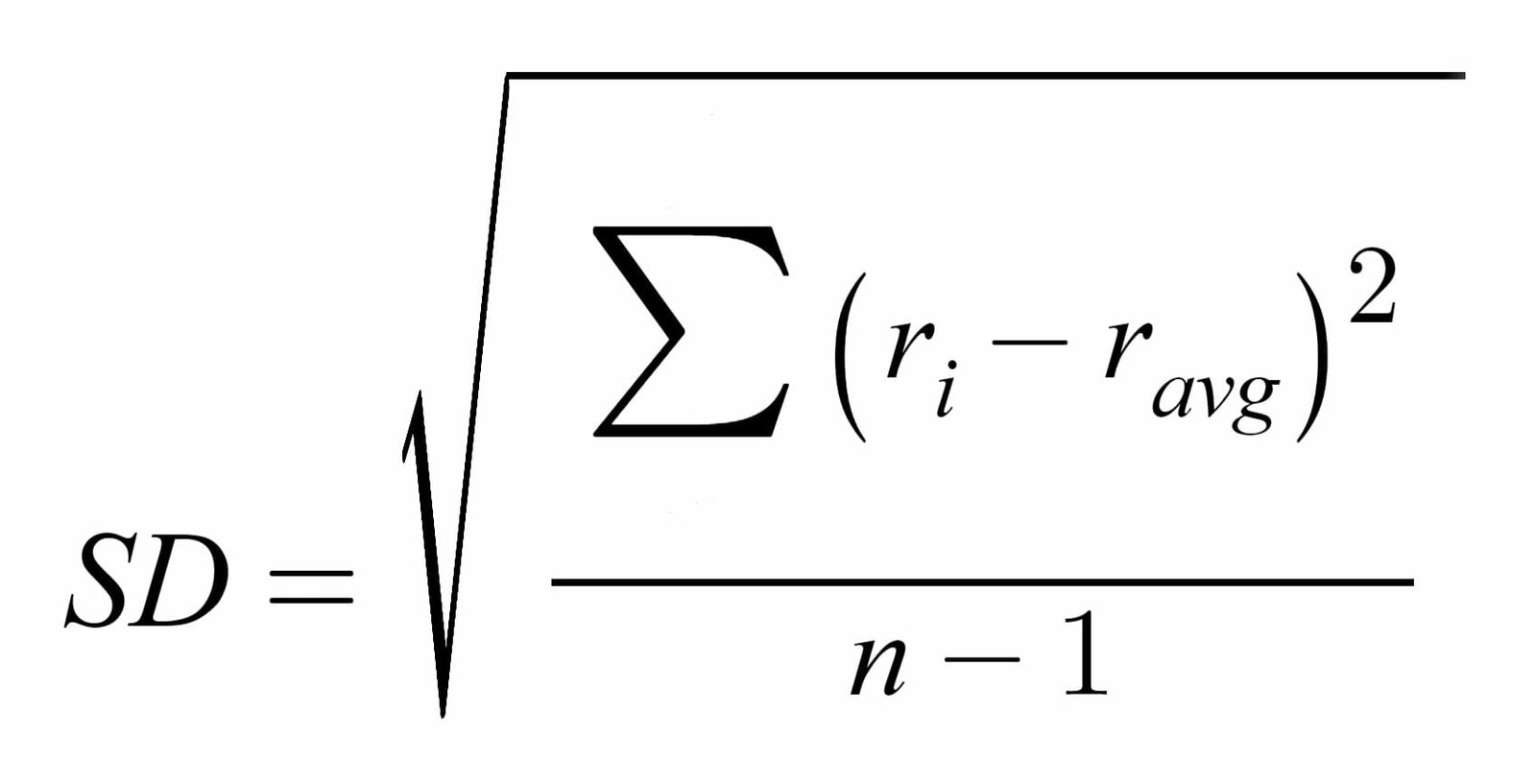
Understanding and Calculating Deviation
Deviation occurs when prices move from an expected range of reactions. The expected norm found in any range of data is called a mean average. The average sum of a changing stock price is its mean average. The price actions that occur above or below this average are considered variances. Standard deviation is specifically calculated as the square root of variance. According to tastytrade, deviation can help you to measure your risks.
What Is Standard Deviation?
Measuring the variances in a set of data calls for a standard to be established. The mean average of a data set, like an average stock price, is a common standard used to measure deviance. Through deviance, investors aim to understand how much prices are moving regardless of a specific direction. Markets that move in increments of $5.00, for example, show different data traits than a market moving in increments of $.30 cents in each price rally.
Deviation formulas for populations and samples
When using a formula based on population deviation, the equation calls for every individual in the population to be formulated via a standard digit. Sample deviations, instead, use statistical modeling, which is to generalize or isolate only some individuals in a population. In the case of investing, population deviations enable you to account for each data point in the info you gather. Additionally, there’s a common rule in deviation: high deviation comes only from volatile prices.

Steps for calculating deviation
Standard deviation is calculated as follows:
- Add all of the individual points of data together, and then divide them by the total number of each individual point.
- The resulting number is your mean and must be subtracted from each individual data point.
- The integers you get for each data point is then squared and then divided by the number of total data points one more time.
- Now subtract each data integer by one.
It still helps to get a visual regarding how the data looks once it’s being calculated. Therefore, let’s say that 6, 4, 9 and 3 are different prices of one stock over the past four hours. The total number of individual data points used equals four, being for each analyzed hour. Four divided by 24 is 6, which is then subtracted from each point, resulting in 0, -2, 3 and -3. Minus each by one.
Why is deviation a useful measure of variability?
The best way to make sense of an investment is to start by assessing its risks. Having a clear view of an asset’s historical volatility gives investors an idea of risk. Deviations that are narrow in nature are less risky and are more stable. Nonetheless, some investors like high deviations and volatile price swings.
Not all volatility is bad for the investor. Consider a better gauge of deviation by measuring variance and using it to assess your investments in the future.




